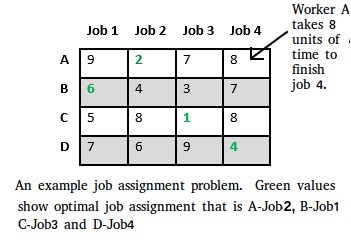
Let there be N workers and N jobs. Any worker can be assigned to perform any job, incurring some cost that may vary depending on the work-job assignment. It is required to perform all jobs by assigning exactly one worker to each job and exactly one job to each agent in such a way that the total cost of the assignment is minimized.

Let us explore all approaches for this problem.
We generate n! possible job assignments and for each such assignment, we compute its total cost and return the less expensive assignment. Since the solution is a permutation of the n jobs, its complexity is O(n!).
The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3).
A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem. We can perform depth-first search on state space tree and but successive moves can take us away from the goal rather than bringing closer. The search of state space tree follows leftmost path from the root regardless of initial state. An answer node may never be found in this approach. We can also perform a Breadth-first search on state space tree. But no matter what the initial state is, the algorithm attempts the same sequence of moves like DFS.
The selection rule for the next node in BFS and DFS is “blind”. i.e. the selection rule does not give any preference to a node that has a very good chance of getting the search to an answer node quickly. The search for an optimal solution can often be speeded by using an “intelligent” ranking function, also called an approximate cost function to avoid searching in sub-trees that do not contain an optimal solution. It is similar to BFS-like search but with one major optimization. Instead of following FIFO order, we choose a live node with least cost. We may not get optimal solution by following node with least promising cost, but it will provide very good chance of getting the search to an answer node quickly.
There are two approaches to calculate the cost function:
In this article, the first approach is followed.
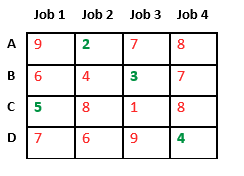
Let’s take below example and try to calculate promising cost when Job 2 is assigned to worker A.
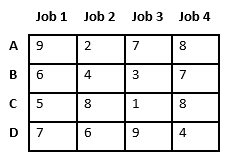
Since Job 2 is assigned to worker A (marked in green), cost becomes 2 and Job 2 and worker A becomes unavailable (marked in red).
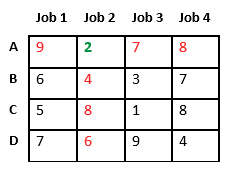
Now we assign job 3 to worker B as it has minimum cost from list of unassigned jobs. Cost becomes 2 + 3 = 5 and Job 3 and worker B also becomes unavailable.
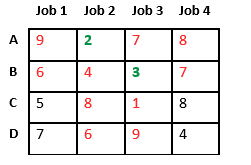
Finally, job 1 gets assigned to worker C as it has minimum cost among unassigned jobs and job 4 gets assigned to worker D as it is only Job left. Total cost becomes 2 + 3 + 5 + 4 = 14.
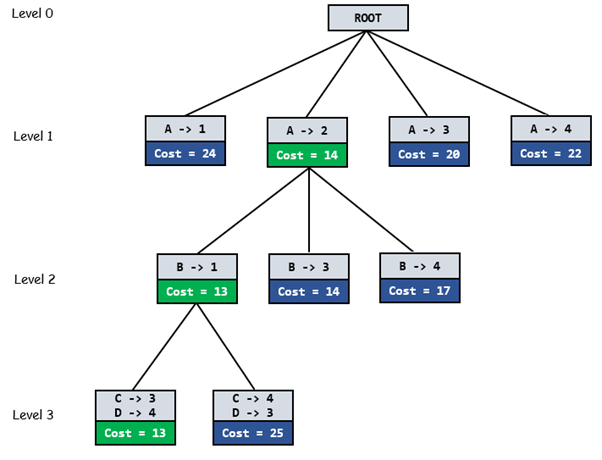
Below diagram shows complete search space diagram showing optimal solution path in green.
Complete Algorithm:
/* findMinCost uses Least() and Add() to maintain the
list of live nodes
Least() finds a live node with least cost, deletes
it from the list and returns it
Add(x) calculates cost of x and adds it to the list
of live nodes
Implements list of live nodes as a min heap */
// Search Space Tree Node
node
int job_number;
int worker_number;
node parent;
int cost;
>
// Input: Cost Matrix of Job Assignment problem
// Output: Optimal cost and Assignment of Jobs
algorithm findMinCost (costMatrix mat[][])
// Initialize list of live nodes(min-Heap)
// with root of search tree i.e. a Dummy node
while (true)
// Find a live node with least estimated cost
E = Least();
// The found node is deleted from the list
// of live nodes
if (E is a leaf node)
printSolution();
return;
>
for each child x of E
Add(x); // Add x to list of live nodes;
x->parent = E; // Pointer for path to root
>
>
>
Below is the implementation of the above approach:
assigned will contains , , , ; , , ;*/ , , , ;*/ Java
Python
store nodes and their costs <span Add the cost of the assigned job to the total cost to Job " " JavaScript
Output :
Assign Worker A to Job 1
Assign Worker B to Job 0
Assign Worker C to Job 2
Assign Worker D to Job 3
Optimal Cost is 13
Time Complexity: O(M*N). This is because the algorithm uses a double for loop to iterate through the M x N matrix.
Auxiliary Space: O(M+N). This is because it uses two arrays of size M and N to track the applicants and jobs.